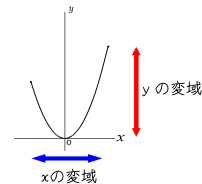
変化の割合とは 1分でわかる意味 公式 傾きと増加量との関係
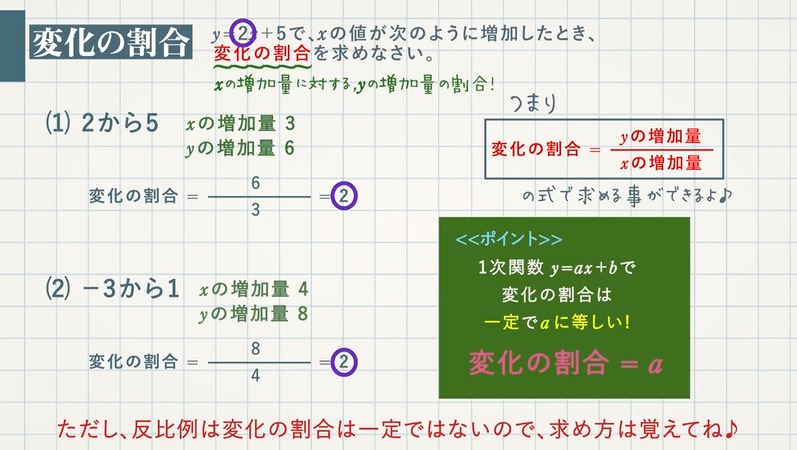
関数 \(y=ax^2\)について、\(x\)の値が\(m\)から\(n\)まで増加したときの変化の割合を考える。 基本形の解き方通りに考えてみると 表はこのようになります。変化の割合= yの増加量 xの増加量 比例反比例、1次関数、そして2乗に比例する関数、 変化の割合 はすべて同じ式を用いる。 ただし、1次関数では変化の割合は一定だが、 2乗に比例する関数では変化の割合は一定にならない。 y=3x2 についてそれぞれの場合の変化の割合をもとめる。 xが−3から1まで変化するとき xが1から5まで変化するとき ① xが3から1まで変化するときの変化の割合 x=3のとき
二次関数 グラフ 平行移動 公式
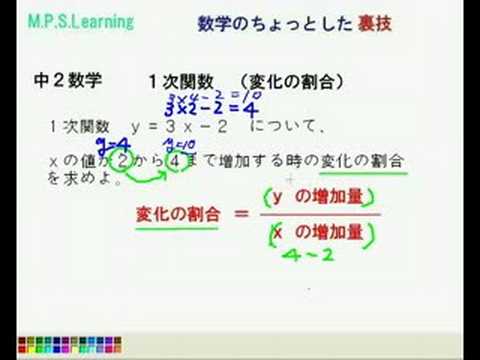
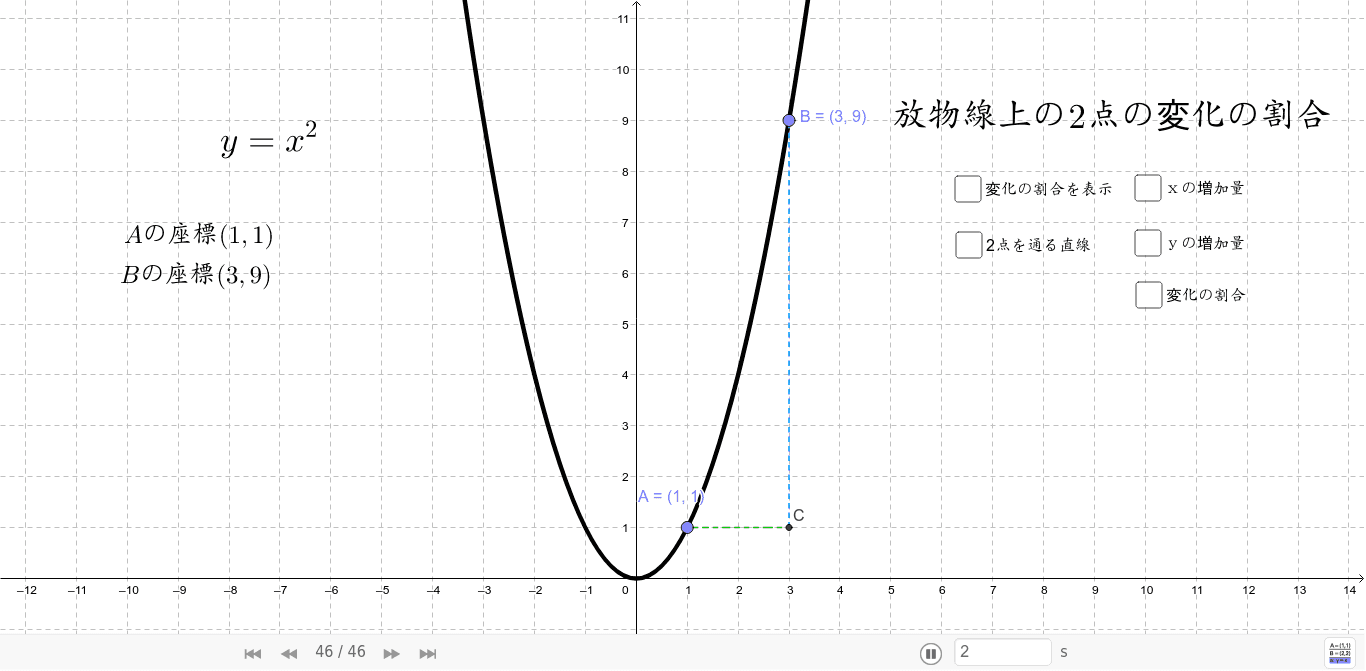
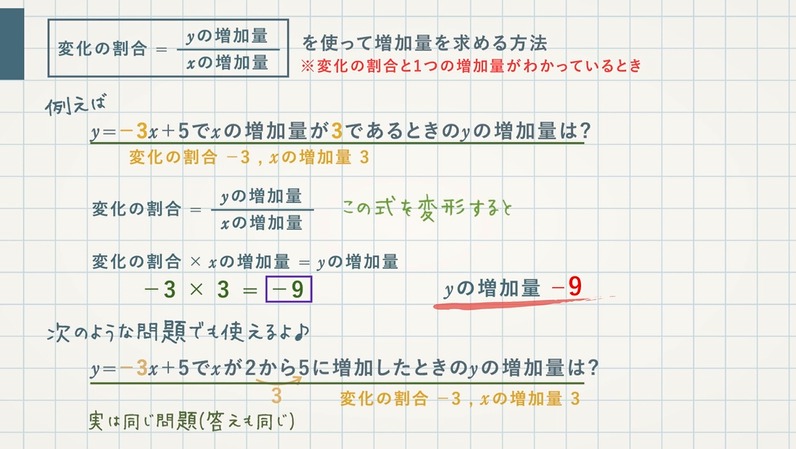
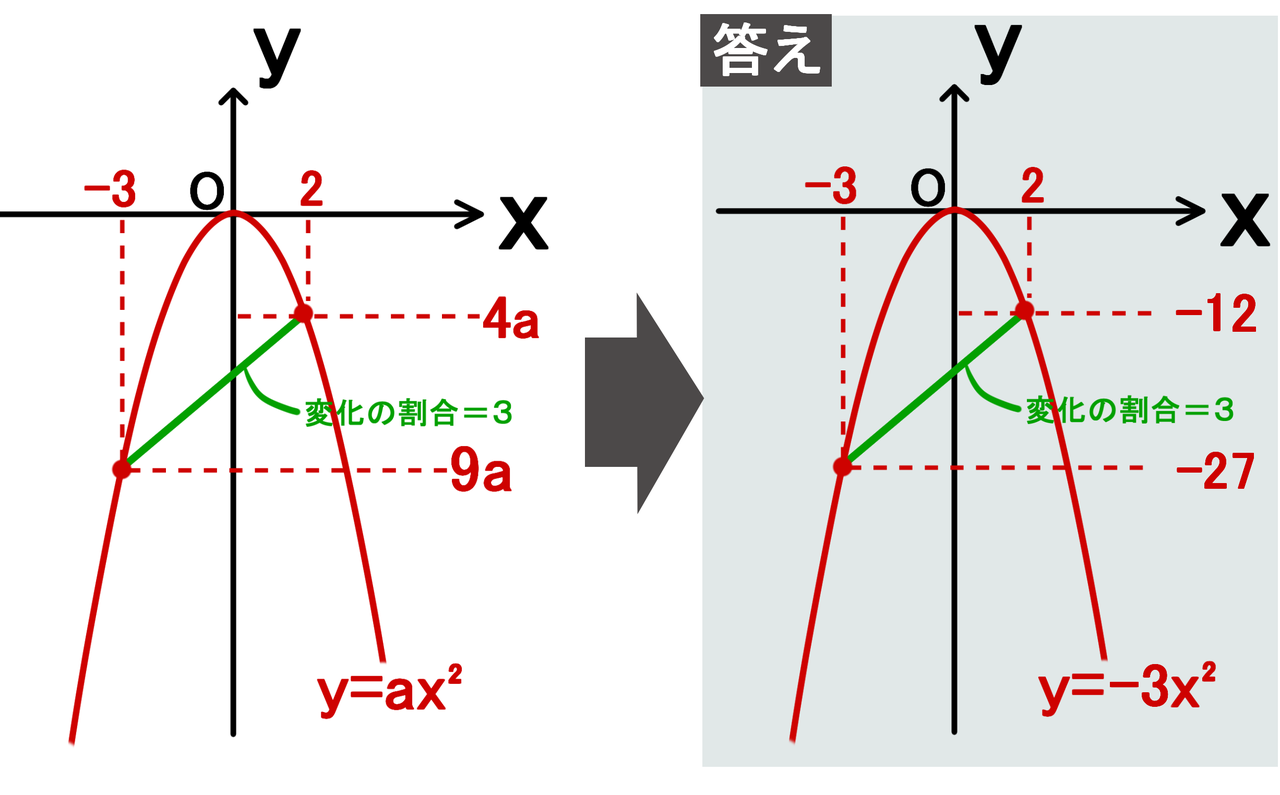
二次関数 グラフ 平行移動 公式- 二次関数y=ax2の変化の割合の求め方 には公式があるよ。 xの値がmからnまで増加するとき、変化の割合は、 a (mn) になるんだ。 つまり、 (比例定数)×(xの小さい値 xの大きい値) っていう計算。 簡単だ! さっそく、この公式で変化の割合を求めて というわけで、今回は中3で学習する関数\(y=ax^2\)の単元から 「平均の速さを求める」 についてイチから解説していくよ。 具体的には次のような問題のことだね。
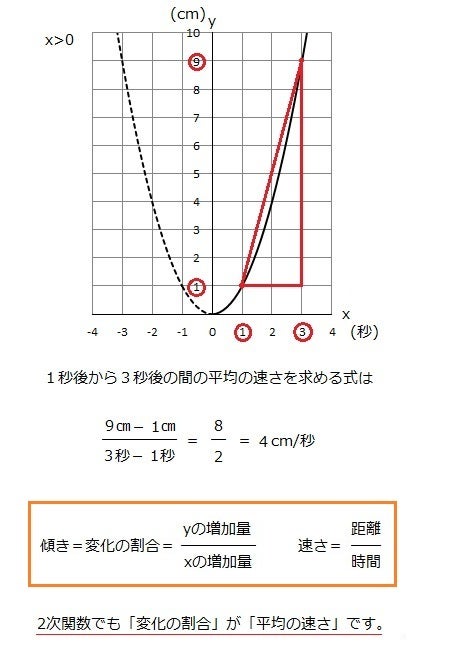
平均の速さは変化の割合 傾き 永和進学ゼミ 個別指導ソフィア 学習塾ブログ
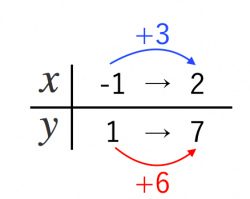
変化の割合= yの増加量 xの増加量 変 化 の 割 合 = y の 増 加 量 x の 増 加 量 なので、この式に代入します。 変化の割合= ax2 2 −ax2 1 x2 −x1 変 化 の 割 合 = a x 2 2 − a x 1 2 x 2 − x 1 分子を a a でくくると 変化の割合= a(x2 2 −x2 1) x2 −x1 変 化 の 割 合(2)(1)を用いて,関数 のxの値が4から2まで増加するときの変化の割合を求めなさい。 解説・解法 y=ax 2 の変化の割合の中でも少し応用編というか,発展編です。教科書には載っていませんが,この公式を覚えておいたら楽に点数が取れます。 新しい関数として 「 = y = a x 2 」を 学習しましたね 中3数学「関数 = y = a x 2 」の問題 どこよりも簡単な解き方・求め方 「関数」は、中1で「比例」、中2で「一次関数」を学習しましたね 中3では「2乗に比例する関数」を一緒に見ていきましょう
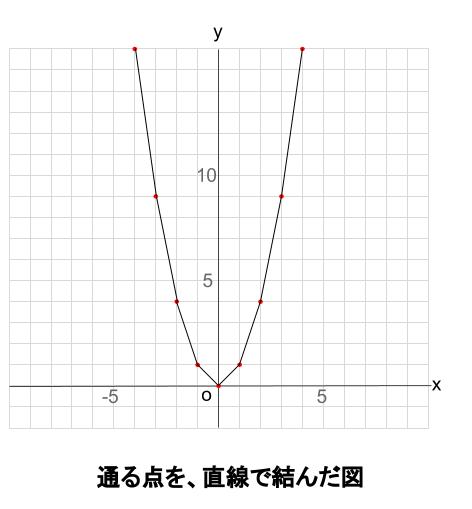
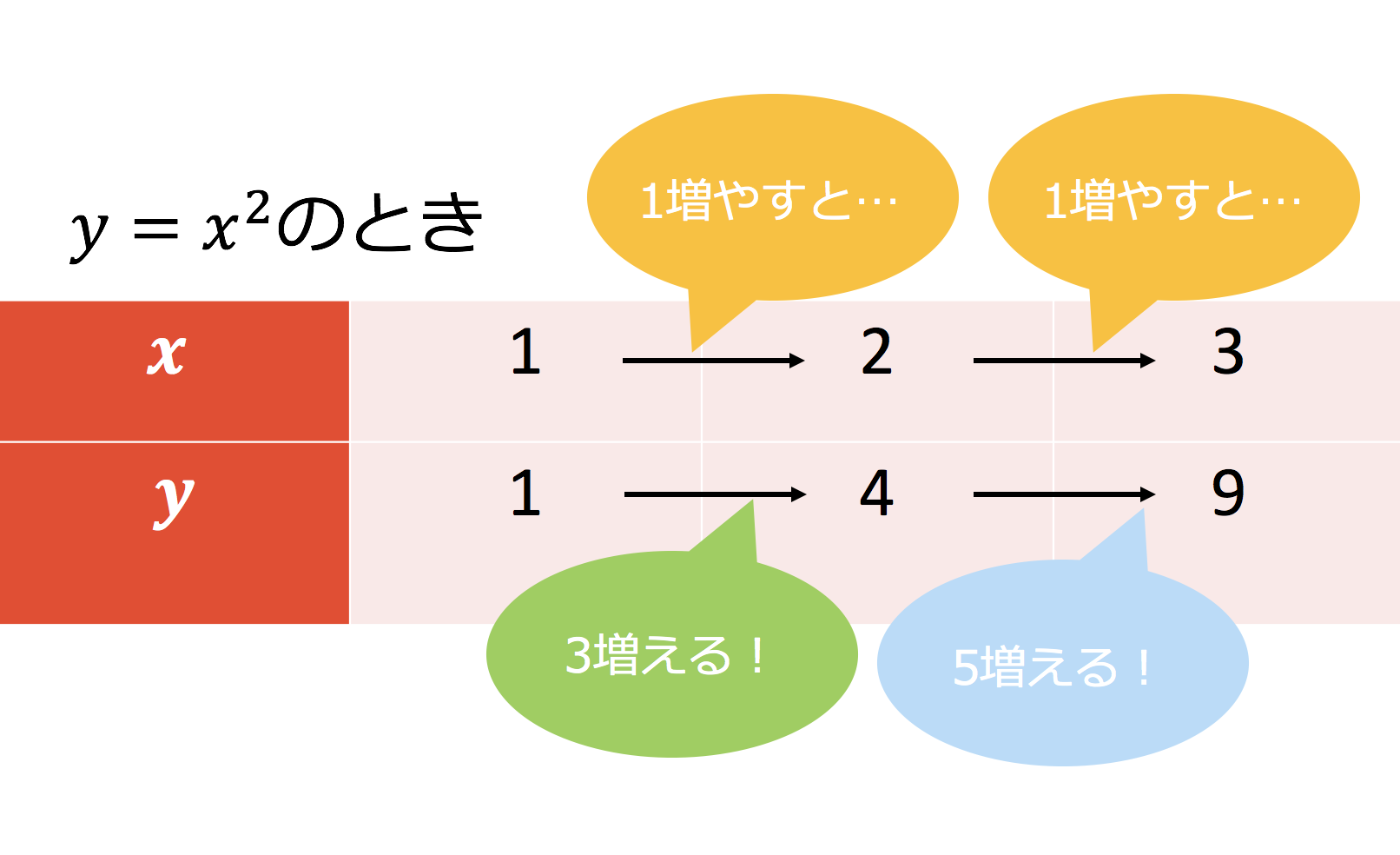
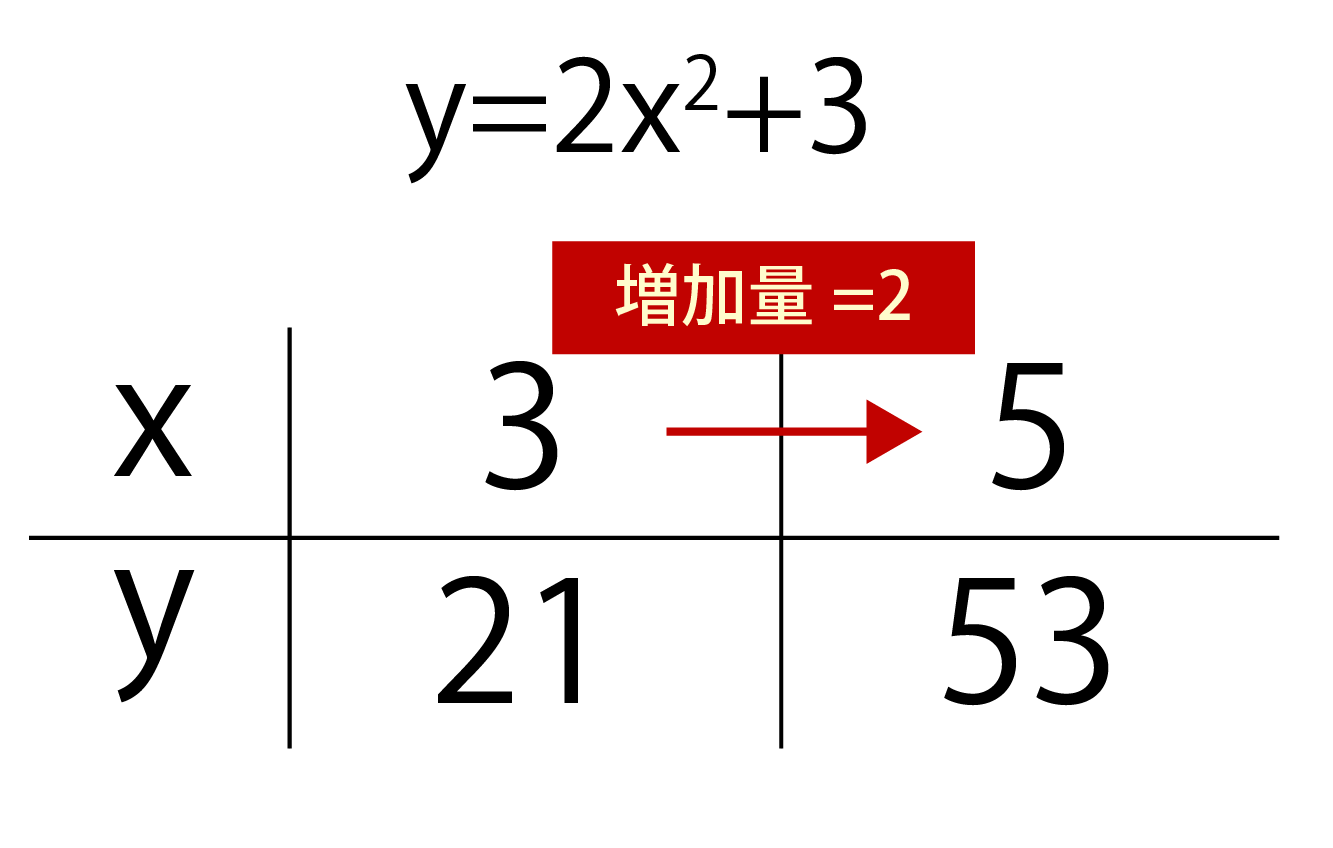
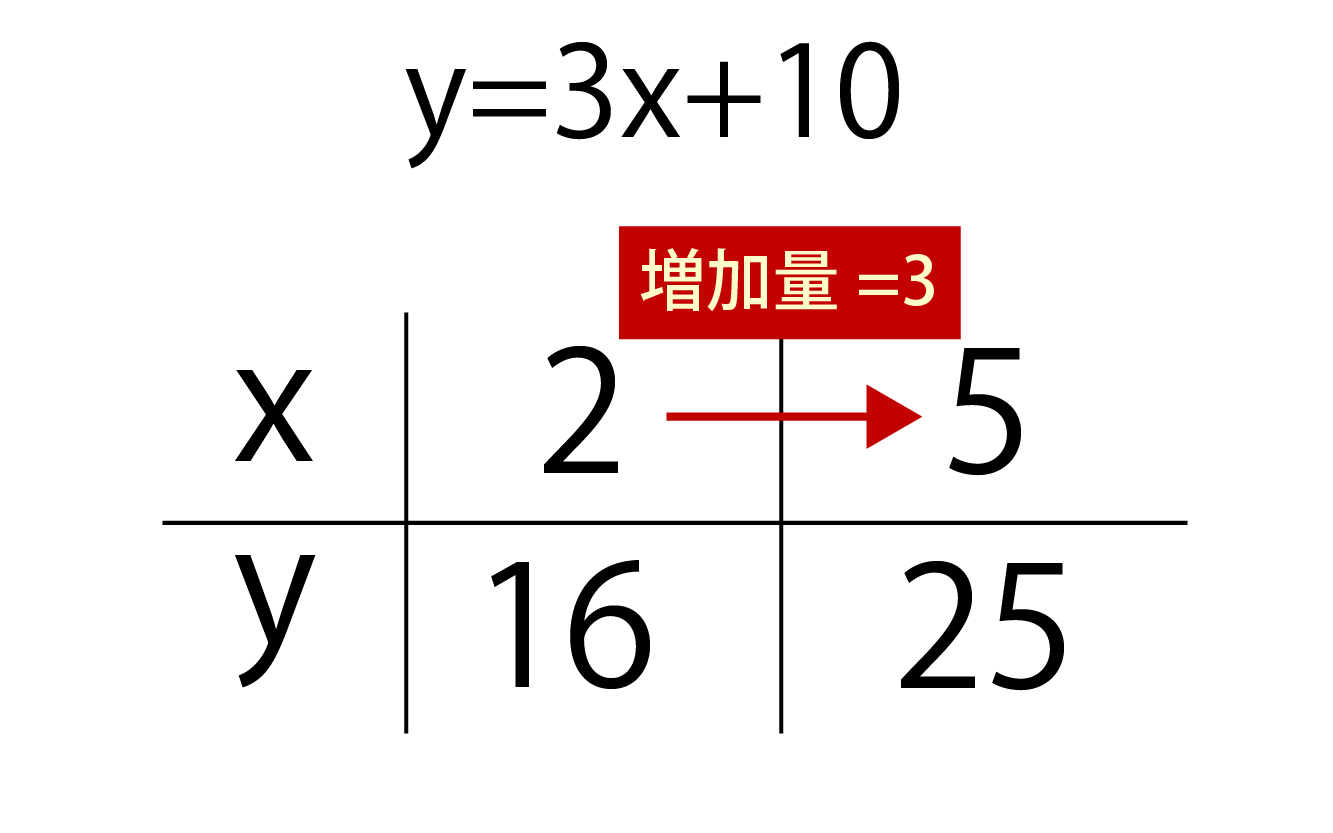
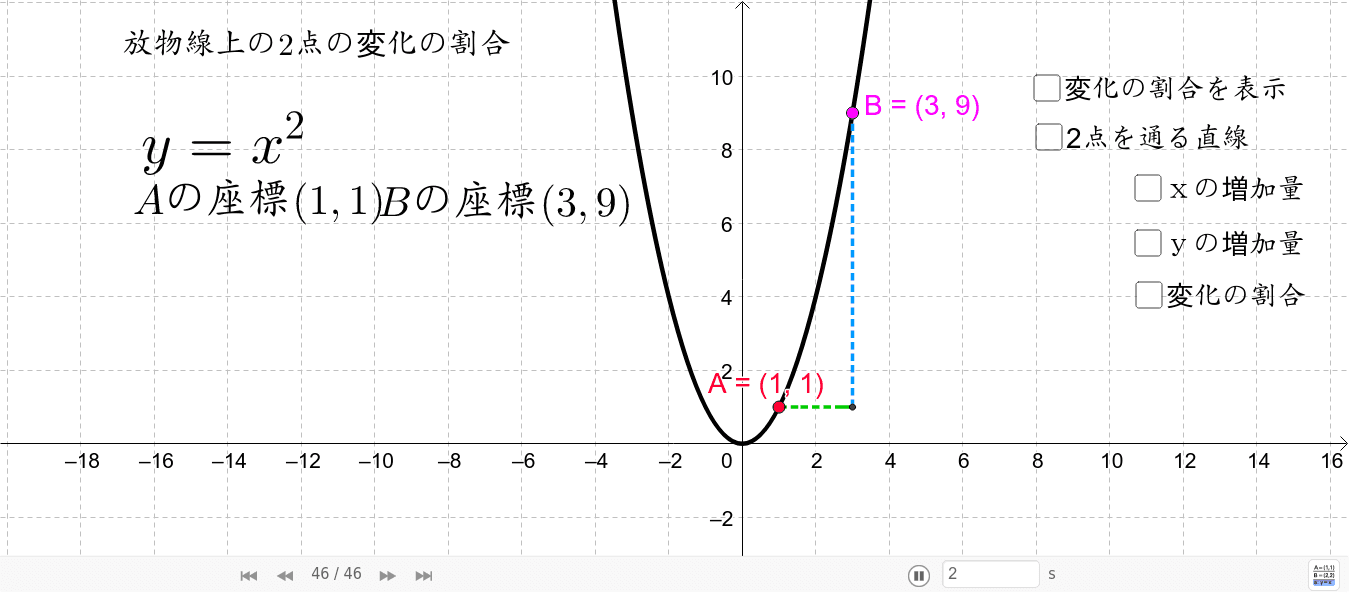
2乗に比例する関数 変化の割合 2乗に比例する関数 変化の割合の問題です。 1次関数 y=axb では変化の割合がaで一定になります。 y=ax 2 の場合は 変化の割合は一定にはなりません 。 変化の割合は 例) y=2x 2 について ⑴ xが1から3まで変化するとき xの増加量=31=2 yの増加量=2×3 2 2×1 2 =16 変化の割合=16/2=8 ⑴ xが1から3まで変化するとき xの増加量=3 (1)=4 y今回は、「y=ax 2 のグラフの変化の割合」について考えるよ。 中学2年生の「1次関数」の学習でも出てきた「 変化の割合 」って言葉、覚えているかな?変化の割合のポイントは! 変化の割合とは、x の増える量に対して、y がどれだけ増えたかを示す割合で、( y の増加量 ) / ( x の増加量) で求める
二次関数 グラフ 平行移動 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | 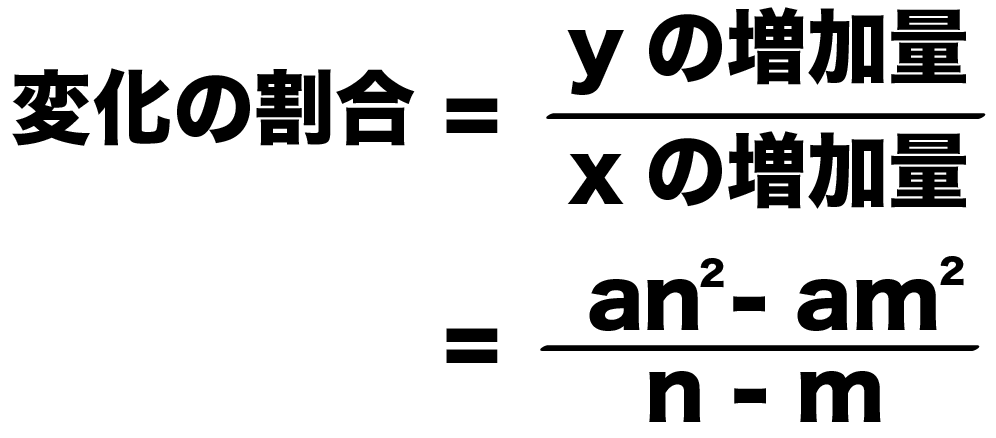 |  |
 | ||
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 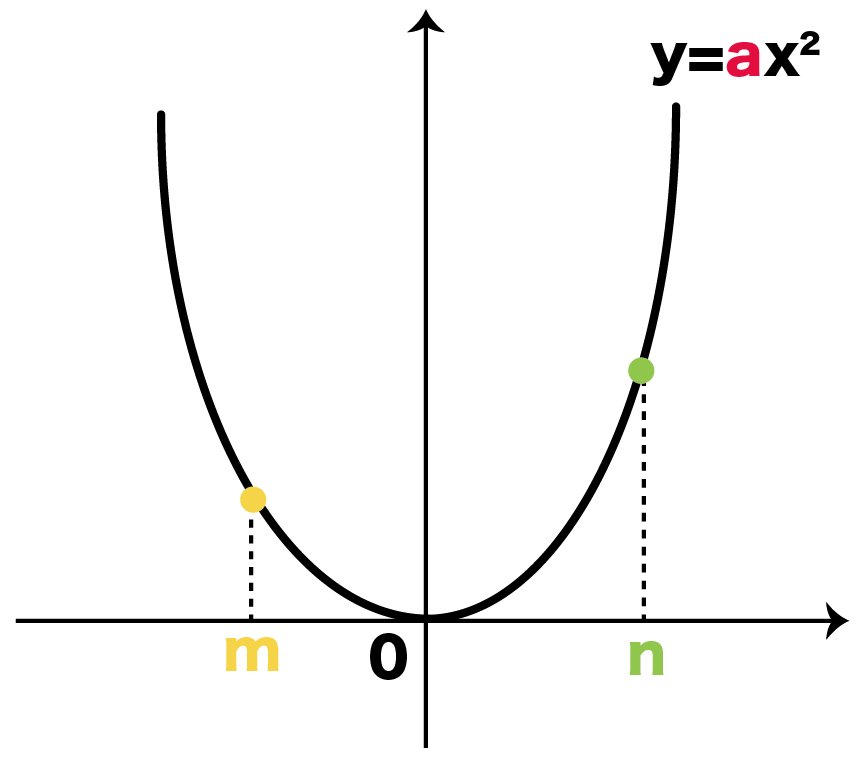 |
 |  |  |
 | ||
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
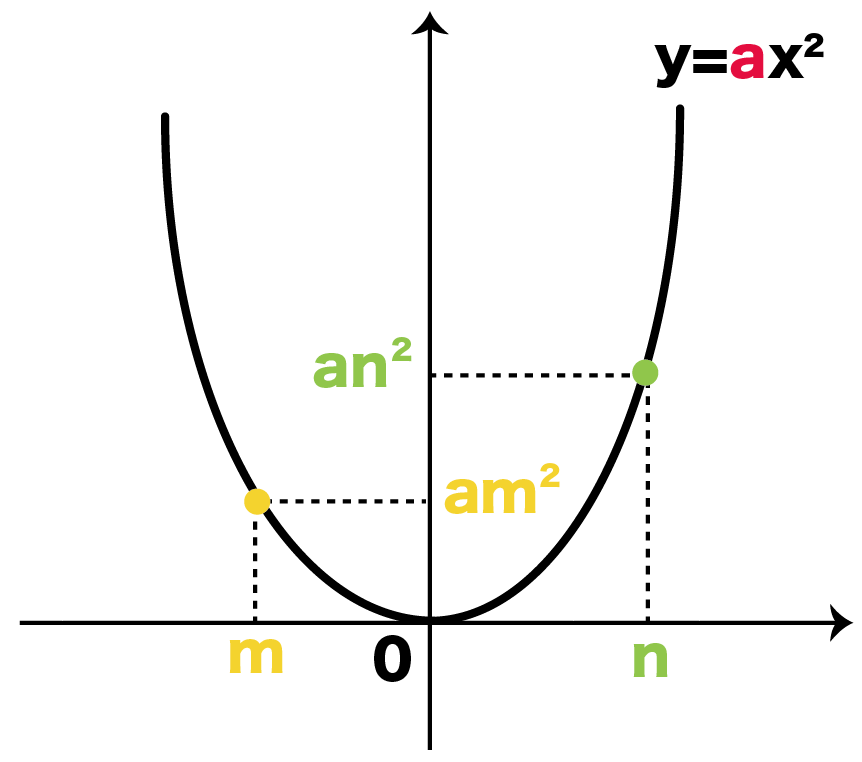 |  | |
 |  |  |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「二次関数 グラフ 平行移動 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 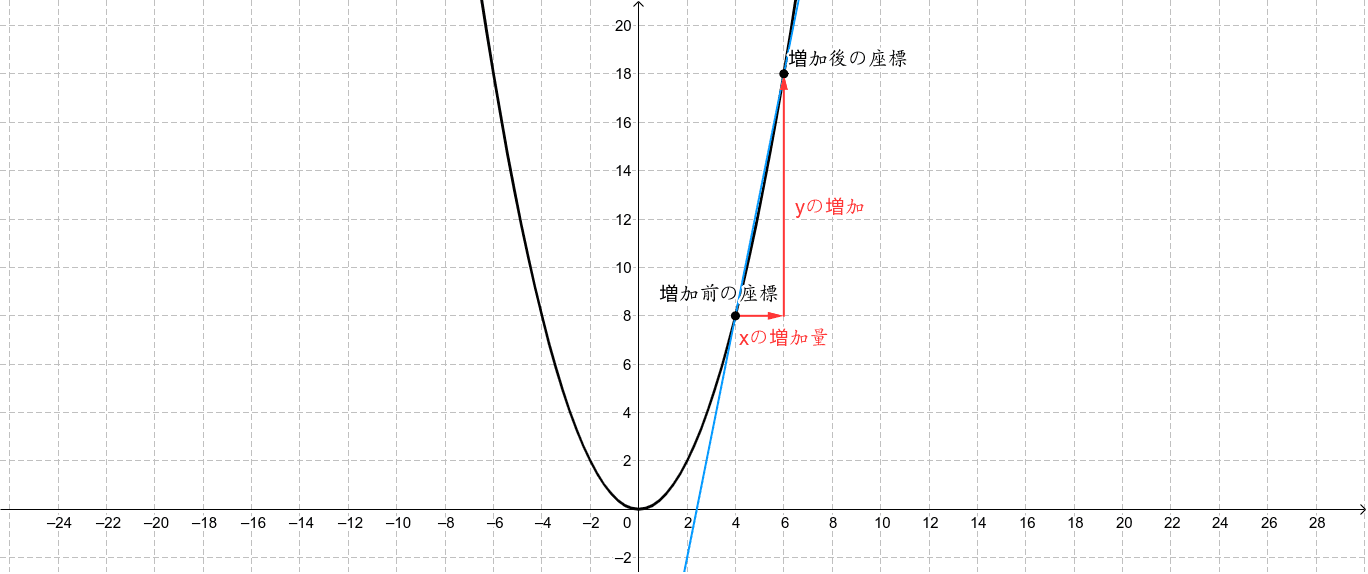 |
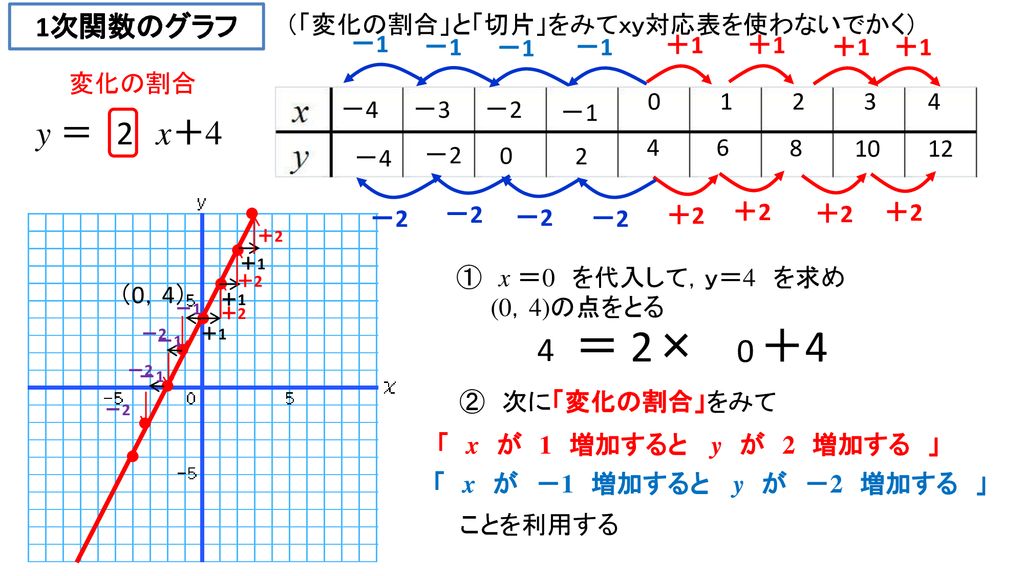
変化の割合を計算してみます。 x の増加量= 2-0 =2 y の増加量= 8-0 =8 ですから、 変化の割合= 8÷2 =4 このように、簡単に求められます。 そして、計算の結果、 この場合の「変化の割合」は 「4」 なので、 "a の値"とは違うものですね。 ですから、y=ax² では、 ・ "a"は「比例定数」とは呼べるが、 ・ 「変化の割合」とは言えない。 (⇒ 「変化の割合」 は、 計算しないと分からない 。※以上のような訳で,1次関数(直線)の変化の割合は, x の係数を見たら即答え ですが,この裏技は直線の場合しか使えないので,反比例のグラフや3年生で習う2次関数のグラフでも真似してしまうと間違います. だから,どんな問題でも対応できるようにするには,地道に
Incoming Term: 二次関数 定義域 場合分け 問題, excel 2次関数 係数 関数, エクセル 関数 2次関数 係数, 二次関数 最大値 場合分け 2つ 3つ, 二次関数 範囲 a 異なる 2点, excel 二次関数 係数 求める, 二次関数 一次関数 交点 問題, 二次関数 グラフ 平行移動 公式, 数1 二次関数 軸 動く 問題, 二次元配列 関数 ポインタ 引数, 二次関数 最大値 最小値 場合分け, 中二 数学 一次関数の利用 問題,




0 件のコメント:
コメントを投稿